Geometry Transformation: Translations, Reflections, and Rotations

✓

TL,DR

Translations move every part of a figure some horizontal and vertical distance.

Reflections flip a figure over a line of reflection.

Rotations spin a figure around a point by a set angle, following the same rules every time.

Transformations in Geometry are important because they set the visual frame for congruence, which ends up opening the door for the rest of the course which focuses heavily on solving shapes. The trick to transformations is to focus on the defined rules on a coordinate grid.

Transformations in high school Geometry initially focus on isometries, which are rigid motion transformations. In english, this means moving a shape across space without distorting its sides or angles. You can slide (translate), flip (reflect) or spin (rotate), all without distorting the sides of the shapes.

---

• Translations

• Rotations

• Reflections

---

Put a paper triangle on the table. Say slide, flip, turn. Slide it right and up while you say the distances. Flip it over a ruler to show a mirror line. Turn it around a pencil point. Ask, what stayed the same, size and shape. What changed, position or orientation. Keep it playful for two minutes.

Draw a coordinate plane. Plot three points for a triangle. Use arrows to show a translation vector, example, right 3, down 2. Say the sentence frame, every point moves 3 right and 2 down. Write new coordinates under each point. Check that side lengths match the original.

Draw a vertical line as the mirror. Fold the paper on the line if possible, or hold a small mirror there. Count squares to the line and copy that distance to the other side. Name rules as you go, over the y-axis, x becomes opposite, y stays the same. Have your child explain one point out loud.

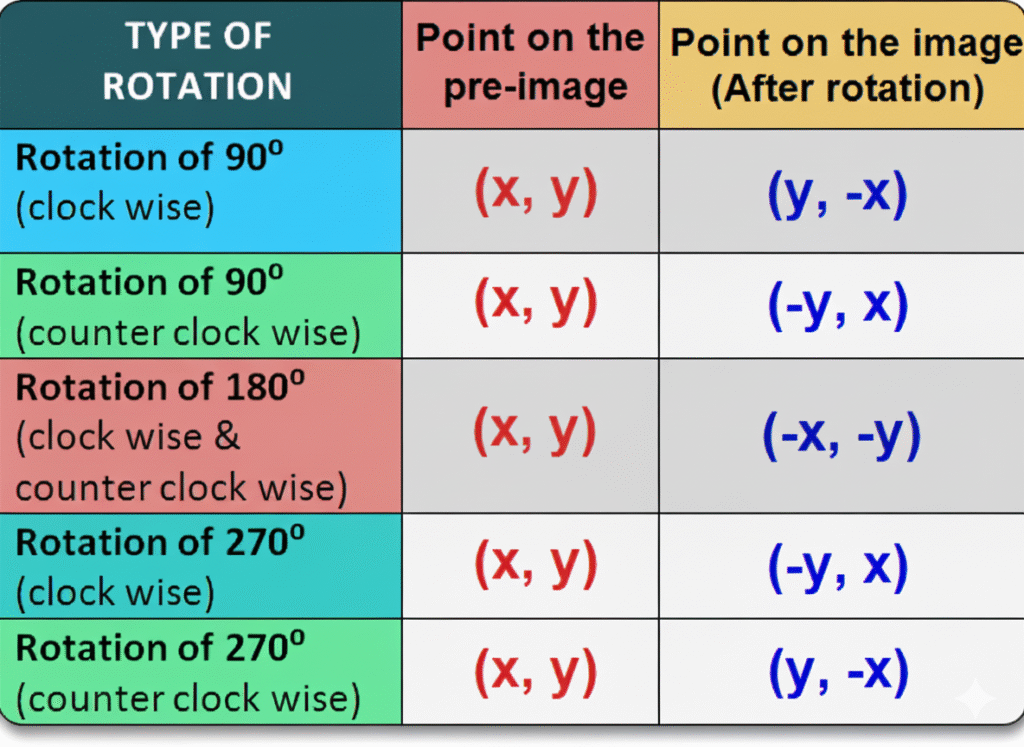
Place tracing paper or clear plastic over the grid. Trace the shape and pin it at the origin. Rotate 90 degrees counterclockwise, then 180, then 270. Say the rule as you rotate, 90 ccw, x and y swap and the new x is the opposite, (x, y) to (−y, x). Compare the tracing to the grid and record the new coordinates.

Use I do, we do, you do. You model one example. Solve one together while your child talks. Then your child solves one and checks with a rule. Prompt thinking, what move, what rule, what point do you start with, how do you know it is correct. Stop at 20 minutes, praise accuracy over speed.

Problem	Answer
Translate A(−2, 1), B(1, 1), C(0, 4) by ⟨3, −2⟩.	A′(1, −1), B′(4, −1), C′(3, 2)
Reflect P(−4, 2) and Q(1, −5) over the y-axis.	P′(4, 2), Q′(−1, −5)
Rotate R(2, −3) 90° counterclockwise about the origin.	R′(3, 2)

---

💡 Before you scroll, here’s what most students slip on during transformations.

Mistake	Fix
Not using the rules from notes to find new ordered pairs	Keep the notes open beside the work. Say each rule aloud before applying it (for example, “x changes sign when reflecting over the y-axis”). Encourage the child to check each new point against the rule.
Capturing the original ordered pairs incorrectly	Have the child label and list each vertex before transforming. Check with the teacher’s diagram or original coordinates before moving anything.
Forgetting to move every point in a translation	Ask, “Did every vertex move the same distance?” Circle any points that were left behind. Reinforce that all points slide equally in a translation.
Mixing up x and y during rotations	Use tracing paper or a coordinate card with x and y labeled. Say the rule each time: 90° ccw means (x, y) → (−y, x). Have the child check one point visually after each rotation.
Drawing the new figure in the wrong quadrant	After plotting, count the quadrants out loud. Ask, “Did we spin or flip into the right one?” Trace the shape lightly before committing in pen or marker.
Not checking for congruence	Place the original and image side by side or overlay them with tracing paper. Confirm all sides and angles match before labeling.

If your child misses three in a row, that’s your signal it’s time for expert support. Book a focused 30-minute session — I’ll pinpoint the exact blocker and build a plan you can keep using at home.

---

Download the free Kuta worksheet

---

---

Q: What is a translation in math?
A: A translation is just a slide. Every point of a shape moves the same distance in the same direction, without turning or flipping. The shape stays congruent.

Q: How do I explain a reflection to my child?
A: Reflections are like mirror images. The shape flips over a line (the line of reflection). Every point is the same distance from that line on both sides.

Q: What is a rotation?
A: A rotation is a turn. The shape spins around a point (usually the origin on a graph). We measure the turn in degrees, such as 90°, 180°, or 270°. The size and shape do not change.

Q: What does “rigid motion” mean?
A: Rigid motions are moves that keep a shape the same size and shape. Translations, reflections, and rotations are all rigid motions. They change where the figure is, but not what it looks like.

Q: How can I explain symmetry at home?
A: Symmetry means a figure can fold onto itself and still match up. Place a mirror or fold the paper along a line. If both halves match, it has line symmetry.

---

Certified math educator and curriculum designer with advanced training in instructional technology. I’ve taught since 2017, both in-person and online, and specialize in turning abstract math into clear, visual steps students actually enjoy.

My mission is to help families build math confidence together — one skill at a time.

I help middle school, high school, and college students master the exact skills that block progress, then build durable habits parents and students can sustain at home.

Serving families in St. Petersburg and online nationwide.